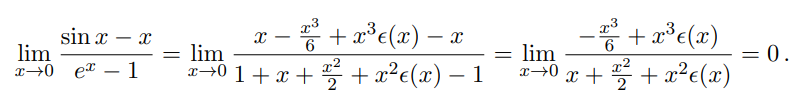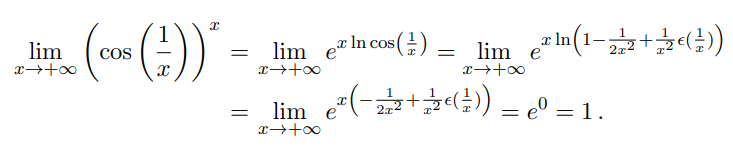Limite

Définition

Fonction d'une variable

Définition :
Soit $l\in\Bbb R$
On dit que $f$ a pour limite $l$ en $x_0$ si $$\forall\epsilon\gt 0,\exists \delta_\epsilon \gt 0 \text{ tq }\forall x\in I,\lvert x-x_0\rvert\lt \delta_\epsilon\Longrightarrow\lvert f(x)-f(x_0)\rvert \lt \epsilon$$
Notation : $\underset{x\to x_0}\lim f(x)=l$

Fonction de plusieurs variables

Définition :
Soit $f:E\subset{\Bbb R}^n\to{\Bbb R}$ une fonction définie au voisinage de $x_0\in{\Bbb R}^n$, sauf peut-être en $x_0$
On dit que $f$ a pour limite $\ell\in\bar{{\Bbb R}}$ en $x_0$ si et seulement si $$\forall\varepsilon\gt 0,\exists\delta\in E,\forall x\in E,\quad\lVert x-x_0\rVert\leqslant\delta\implies\lvert f(x)-\ell\rvert\leqslant\varepsilon$$
On note : $$\displaystyle{\lim_{x\to x_0} } f(x)=\ell\quad\text{ ou }\quad f(x)\underset{x\to x_0}\longrightarrow\ell$$
(Voisinage, R-barre)

Notions liées

Limite infinie en un point
Limite en l'infini
Limite à gauche - Limite à droite

Domaines

Fonction, Fonction de plusieurs variables
Suite réelle
Série numérique

Opérations et théorèmes

Unicité de la limite
Opérations sur les limites
Formes indéterminées
Comparaisons de limites
Théorème de comparaison
Théorème des gendarmes - Théorème de l'encadrement
Limite
Croissances comparées
Critère de Cauchy
Limite d'une fonction composée
Limite le long d'un chemin
Limite en base polaire $${{\underset{n\to+\infty}{\operatorname{lim} }(a_n-b_n)=0}}\iff{{\underset{n\to+\infty}{\operatorname{lim} } a_n=\underset{n\to+\infty}{\operatorname{lim} } b_n}}$$ $${{u_n\lt a}}\implies{{\underset{n\to+\infty}{\operatorname{lim} } u_n\leqslant a}}{\operatorname{lim} }}}$$ $${{u_n\leqslant a}}\implies{{\underset{n\to+\infty}{\operatorname{lim} } u_n\leqslant a}}{\operatorname{lim} }}}$$

Exemples

Calculs de limite en utilisant des DL

(Développement limité)
Exemples : ^[calculer $$\lim_{h\to0}\frac{\sin x-x}{e^x-1}$$

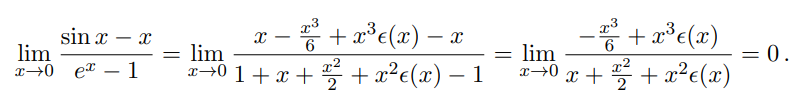
] ^[calculer $$\lim_{x\to+\infty}\left(\cos\left(\frac1x\right)\right)^x$$

]

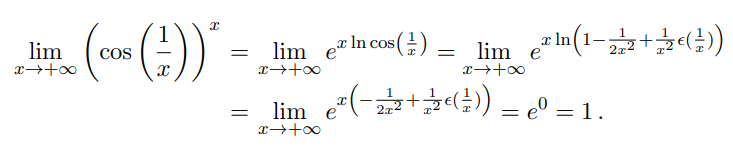
Calcul de limite pour une fonction de plusieurs variables

Soit $f:x,y\mapsto x^2+y\sin(x+y^2)$
En revenant à la définition de la limite, trouvez la limite de $f$ en $(0,0)$

On prend la valeur absolue de $f(x,y)$ pour essayer de revenir à la définition de la limite
$$\begin{align}\lvert f(x,y)\rvert&=\lvert x^2+y\sin(x+y^2)\rvert\end{align}$$

Inégalité triangulaire
$$\leqslant\lvert x^2\rvert+\lvert y\sin(x+y^2)\rvert$$

Car $\sin(x+y^2)\leqslant1$
$$\leqslant\lvert x^2\rvert+\lvert y\rvert$$

Définitions de $a$ et $b$
Soit $\varepsilon\gt 0$. Trouvons $\delta$
On fixe $a=\sqrt{\frac\varepsilon2}$ et $b=\frac\varepsilon2$

Si $x$ et $y$ sont dans les bons intervalles, on a bien $\lvert f(x,y)\rvert\leqslant\varepsilon$
si $x\in]-a,a[$, alors $x^2\leqslant(\sqrt{\frac\varepsilon2})^2\leqslant\frac\varepsilon2$

si $y\in]-b,b[$, alors $\lvert y\rvert\leqslant\frac\varepsilon2$

Donc si $(x,y)\in]-a,a[\times]-b,b[$, alors $$\rvert f(x,y)\lvert\leqslant\lvert x^2\rvert+\lvert y\rvert\leqslant\frac\varepsilon2+\frac\varepsilon2=\varepsilon$$

Conclusion

Soit $\delta=\frac\varepsilon2$. Si $\lVert(x,y)\rVert\leqslant\delta$, alors $(x,y)\in]-a,a[\times]-b,b[$ donc $\lvert f(x,y)\rvert\leqslant\varepsilon$
On a donc bien $$\lim_{(0,0)} f=0$$

(Sinus, Valeur absolue, Inégalité triangulaire)

Exercices

Caractérisation séquentielle de la limite : $${{\lim_{x\to x_0}f(x)=\ell}}\iff{{\left(\forall(u_n)_{n\geqslant0}\subset]a,b[\setminus\{x_0\},u_n\underset{n\to+\infty}\longrightarrow x_0\implies f(u_n)\underset{n\to+\infty}\longrightarrow\ell\right)}}$$
Démonstration : ^[$$
\beginalign&\textsupposons que f(x)\undersetn\to x0\longrightarrow\ell\\ &\textsoit (un)n\in\Bbb N\subset]a,b[\setminus\x0\,un\undersetn\to+\infty\longrightarrow x0\\ &\texton doit montrer que f(un)\undersetn\to+\infty\longrightarrow\ell\\ &\textsoit \varepsilon>0\text. On cherche N\in\Bbb N\text tel que :\\ &n\geqslant N\implies\lvert f(un)-\ell\rvert<\varepsilon\\ &\textcomme f(x)\undersetn\to x0\longrightarrow\ell,\exists\delta>0\text tel que : \\ &\begincases0<\lvert x-x0\rvert<\delta\\ x\in]a,b[\endcases\implies\lvert f(x)-\ell\rvert<\varepsilon\\ &\textcomme un\undersetn\to+\infty\longrightarrow x0:\exists N\in\Bbb N\text tel que n\geqslant N\implies\lvert un-x0\rvert<\delta\\ &\implies\lvert f(un)-\ell\rvert<\varepsilon\\ \\ &\textmontrons maintenant la réciproque :\\ &\textsupposons pour toute suite (un)n\in\Bbb N\subset]a,b[,un\neq x0,n\geqslant0,\\ &un\undersetn\to+\infty\longrightarrow x0\implies f(un)\undersetn\to+\infty\longrightarrow\ell\\ &\textmontrons que f(x)\undersetn\to+\infty\longrightarrow\ell\implies\forall\varepsilon>0,\exists\delta>0:\\ &\begincases0<\lvert x-x0\rvert<\delta\\ x\in]a,b[\endcases\implies\lvert f(x)-\ell\rvert<\varepsilon\\ &\texton raisonne par l'absurde, on suppose \lnot P:\\ &\exists\varepsilon>0,\forall\delta>0,\exists x\in]a,b[,0<\lvert x-x0\rvert<\delta\text et \lvert f(x)-\ell\rvert\geqslant\varepsilon\\ &\texton applique ce qui précède à \delta=\frac1n,n\geqslant1\\ &\forall n\geqslant1,\exists xn\in]a,b[,0,\lvert xn-x0\rvert<\frac1n\text et \lvert f(un)-\ell\rvert\geqslant\varepsilon\\ &\textpar le théorème
des gendarmes, xn\undersetn\to+\infty\longrightarrow x0\\ &\text et de plus, xn\in]a,b[\setminus\x0\,n\geqslant1\\ &\textet comme \lvert f(xn)-\ell\rvert\geqslant\varepsilon,\forall n\geqslant1,f(xn)\undersetn\to+\infty\cancel\longrightarrow \ell\\ &\textil y a une contradiction\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\square\endalign$$]
Limite à gauche - Limite à droite

Math'φsics

Formulaire de report