Convolution - Math'φsics

Convolution

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent

Convolution de \(f*g\)
Fonction qui renvoie l'aire sous la courbe du produit des deux fonctions, lorsqu'on retourne la deuxième et qu'on la translate par \(x\) : $$f*g(x):=\int_{{\Bbb R}^d}f(h)g(x-h)\,dh$$
- bien définie si \(f\in L^1({\Bbb R}^d)\) \(g\in L^p({\Bbb R}^d)\), avec \(p\in[1,+\infty]\)
- on a alors \(\lVert f*g\rVert_1\) \(\leqslant\lVert f\rVert_1\lVert g\rVert_p\)
- dérivation : si \(g\) \(\in\mathcal C^k_c({\Bbb R}^d)\), alors \(\partial_\alpha(f*g)=\) \(f*\partial_\alpha g\) \(\forall\alpha\in{\Bbb N}^d\) tel que \(\lvert\alpha\rvert\leqslant k\)
- support : \(\operatorname{supp}(f*g)\) \(\subset\overline{\operatorname{supp}(f)+\operatorname{sup}(g)}\)
- si \(f,g\in L^2([-\pi,\pi])\), alors \(c_n(f*g)=\) \(2\pi c_n(f)c_n(g)\) et la Série de Fourier de \(f*g\) converge uniformément vers \(f*g\)
Questions de cours

Démontrer :

On fait d'abord plein de suppositions.

On applique l'Inégalité de Jensen avec \(x\mapsto x^p\) et \(\mu=f(h)\,dh\).

On retrouve alors facilement les normes en isolant les variables.

Ok pour \(\inf f\ne1\) par homogénéité.

Et on peut se débarrasser de l'hypothèse de positivité en passant aux valeurs absolues.

Démontrer :

Ecrire sous forme intégrale.

On applique l'Inégalité de Jensen avec \(x\mapsto x^p\) et \(\mu=f(h)\,dh\).

On conclut en changeant l'ordre des intégrales via le Théorème de Fubini.

START
Ω Basique (+inversé optionnel)
Recto: Justifier l'appellation "produit de convolution".
Verso: On a trois propriétés :

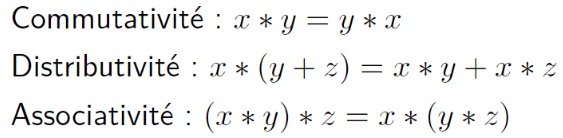
Bonus:
Carte inversée ?:
END

Appliquer l'Inégalité de Cauchy-Schwarz nous permet de dire que la convolution est bornée et dans \(L^2\).

L'égalité des coefficients s'obtient en appliquant le Théorème de Fubini-Lebesgue plusieurs fois.

Une majoration de ce terme via \(ab\leqslant a^2+b^2\) nous permet de dire que la série de Fourier de \(f*g\) converge uniformément vers une limite continue \(F\).

\(f*g\) est donc continue en tant que fonction égale presque partout à une fonction continue (car \(f*g\) et \(F\) sont limites de \((F_N)_N\)).

START
Ω Basique (+inversé optionnel)
Recto: Explique pourquoi la formule \(c_n(f*g)=2\pi c_n(f)c_n(g)\) explique l'effet régularisant de la convolution.
Verso: Les coefficients de haute fréquence de \(f*g\) tendent plus vite vers \(0\) lorsque \(n\to+\infty\), puisque ceux de \(c_n(f)\) et \(c_n(g)\) tendent vers \(0\) lorsque \(n\to+\infty\).
Bonus:
Carte inversée ?:
END

On est bien dans \(L^1\) puisque \(g\in\mathcal S\).

Pas besoin de le montrer pour tous les multi-indices, on peut juste le montrer pour un seul et conclure par récurrence.

On fait une variation en écrivant la Formule de Taylor-Lagrange.

Changement de variable.

Développement limité.

On obtient une borne sur la dernière intégrale en reconnaissant qu'elle est sous forme d'une convolution et en utilisant un résultat précédent.

START
Ω Basique (+inversé optionnel)
Recto: Quel genre d'opérateur \(T\) peut être écrit comme une convolution ?
Verso: Tout opérateur linéaire, continu et invariant par translation \(T\) peut être exprimé de cette manière.
Bonus: I.e. \(Tu=g*u\) pour un certain noyau \(g\).
Théorème de Riesz-Fréchet Carte inversée ?: y
END

Exercices

Posons \(B_0=\Bbb 1_{[0,1[}\), puis par récurrence \(B_{n+1}=B_n*\Bbb 1_{[0,1[}\).
Montrer que pour \(n\geqslant1\), \(B_n\) est de classe \(\mathcal C^{n-1}\). Quel est le support de \(B_n\) ?

On va procéder par récurrence \(\to\) initialisation ok.

Pour l'hérédité, on simplifie l'expression via un changement de variable.

On peut réécrire cette égalité pour utiliser le Théorème fondamental d'analyse pour démontrer la régularité.

Idem pour le support, ça se montre rapidement par récurrence.

Soient \(f,g\in L^2({\Bbb R}^d)\).
Montrer que \(f*g(x)\) est bien défini pour tout \(x\in{\Bbb R}^d\).

C'est immédiat en utilisant l'Inégalité de Cauchy-Schwarz.

Soient \(f,g\in L^2({\Bbb R}^d)\).
Montrer que \((f,g)\mapsto f*g\) est continue de \(L^2\times L^2\) dans \(L^\infty\).

On a une majoration de la norme en passant au \(\sup\) dans l'Inégalité de Cauchy-Schwarz.

On conclut par bilinéarité.

On considère l'opérateur \(\varphi\), qui associe à \(u\) \(T(u)(0)\).

C'est une forme linéaire continue.

On l'écrit via le Théorème de représentation de Riesz.

On prend un changement de variable qui fait apparaître une convolution.

Le résultat se généralise à tout \(a\ne0\) par invariance de \(T\) par translation.
Rétroliens :